Profª Marlene Shimabuku, Colégio Estadual Anita Garibaldi - Ensino Fundamental e Médio, Jardim Alegre/PR.
domingo, 6 de novembro de 2011
sábado, 29 de outubro de 2011
domingo, 23 de outubro de 2011
Números Complementares
Forme pares com bolinhas que somem 10 para eliminá-las do tabuleiro.

Jogar "Números Complementares"

Jogar "Números Complementares"
Como jogar "Números Complementares"
Você deve escolher duas bolinhas cuja soma dê 10 e que estejam conectadas por uma linha que faz no máximo duas curvas.
O objetivo é eliminar o máximo possível de bolinhas, no menor tempo possível.
O objetivo é eliminar o máximo possível de bolinhas, no menor tempo possível.
Balança Lógica
A partir das posições das balanças é possível determinar, logicamente, qual é o objeto com maior massa ("mais pesado").
 Jogar "Balança Lógica"
Jogar "Balança Lógica"
 Jogar "Balança Lógica"
Jogar "Balança Lógica"Como jogar "Balança Lógica"
Determine qual é o objeto mais pesado fazendo, de cabeça, equações ou inequações simples.
Tangram
Tangram é um puzzle chinês muito antigo, o nome significa "Tábua das 7 sabedorias". Ele é composto de sete peças (chamadas de tans) que podem ser posicionadas de maneira a formar um quadrado: 5 triângulos de vários tamanhos, 1 quadrado e 1 paralelogramo.
Neste puzzle deve-se seguir duas regras: usar todas as peças e não sobrepor as peças.
Tangram
Neste puzzle deve-se seguir duas regras: usar todas as peças e não sobrepor as peças.
Tangram
sábado, 9 de julho de 2011
terça-feira, 15 de março de 2011
Jogo das Contas
Pratique neste jogo as 4 operações fundamentais (adição, subtração, multiplicação e divisão) e tente virar um Gênio da Matemática!
Clique na imagem abaixo para jogar. Boa sorte!
Clique na imagem abaixo para jogar. Boa sorte!
Frações
Frações
Chamamos:
-
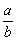 de fração;
de fração; - a de numerador;
- b de denominador.
Veja um exemplo:
A fração
Durante muito tempo, os números naturais foram os únicos conhecidos e usados pelos homens. Depois começaram a surgir questões que não poderiam ser resolvidas com números naturais. Então surgiu o conceito de número fracionário.
O significado de uma fração
Uma fração envolve a seguinte idéia: dividir algo em partes iguais. Dentre essas partes, consideramos uma ou algumas, conforme nosso interesse.
Exemplo: Roberval comeu

Na figura acima, as partes pintadas seriam as partes comidas por Roberval, e a parte branca é a parte que sobrou do chocolate.
Jogo
Agora é hora de se exercitar! Ajude o arqueiro a acertar os balões com as frações correspondentes.
Clique na imagem abaixo para jogar. Boa sorte!
sexta-feira, 11 de março de 2011
Jogo - Compras da Zulu
1. Confira o valor em dinheiro que você tem.
2. Clique nos produtos para colocar no carrinho e clique novamente para retirar.
3. Você deve gastar exatamente o valor do dinheiro. Se ultrapassar esse valor você perderá uma vida.
Boa sorte!
Clique na imagem abaixo para jogar!
2. Clique nos produtos para colocar no carrinho e clique novamente para retirar.
3. Você deve gastar exatamente o valor do dinheiro. Se ultrapassar esse valor você perderá uma vida.
Boa sorte!
Clique na imagem abaixo para jogar!
Jogo da Matemática
A bruxa Anoréxica raptou o Rei Apetite. Para salvá-lo você deve seguir o caminho até a casa da bruxa resolvendo as contas. Use as setas para movimentar os personagens. Boa sorte!
Clique na imagem abaixo para jogar!
Clique na imagem abaixo para jogar!
sexta-feira, 4 de março de 2011
Números Primos
Números primos são os números naturais que têm apenas dois divisores diferentes: o 1 e ele mesmo.
Exemplos:
1) 2 tem apenas os divisores 1 e 2, portanto 2 é um número primo.
2) 17 tem apenas os divisores 1 e 17, portanto 17 é um número primo.
3) 10 tem os divisores 1, 2, 5 e 10, portanto 10 não é um número primo.
1) 2 tem apenas os divisores 1 e 2, portanto 2 é um número primo.
2) 17 tem apenas os divisores 1 e 17, portanto 17 é um número primo.
3) 10 tem os divisores 1, 2, 5 e 10, portanto 10 não é um número primo.
Observações:
=> 1 não é um número primo, porque ele tem apenas um divisor que é ele mesmo.
=> 2 é o único número primo que é par.
=> 1 não é um número primo, porque ele tem apenas um divisor que é ele mesmo.
=> 2 é o único número primo que é par.
Os números que têm mais de dois divisores são chamados números compostos.
Exemplo: 15 tem mais de dois divisores => 15 é um número composto.
Exemplo: 15 tem mais de dois divisores => 15 é um número composto.
- Reconhecimento de um número primo
=> ou uma divisão com resto zero e neste caso o número não é primo,
=> ou uma divisão com quociente menor que o divisor e o resto diferente de zero. Neste caso o número é primo.
Exemplos:
1) O número 161:
- não é par, portanto não é divisível por 2;
- 1+6+1 = 8, portanto não é divisível por 3;
- não termina em 0 nem em 5, portanto não é divisível por 5;
- por 7: 161 / 7 = 23, com resto zero, logo 161 é divisível por 7, e portanto não é um número primo.
- não é par, portanto não é divisível por 2;
- 1+1+3 = 5, portanto não é divisível por 3;
- não termina em 0 nem em 5, portanto não é divisível por 5;
- por 7: 113 / 7 = 16, com resto 1. O quociente (16) ainda é maior que o divisor (7).
- por 11: 113 / 11 = 10, com resto 3. O quociente (10) é menor que o divisor (11), e além disso o resto é diferente de zero (o resto vale 3), portanto 113 é um número primo.
No jogo a seguir, você terá que tentar acertar em todos os números primos de 1 a 25 ou 100. Sempre que errar serão descontados pontos.
Clique na imagem abaixo para jogar!
Quadrado Mágico
Neste jogo, descubra o número que falta, sabendo que a soma por linha, por coluna e por diagonal principal dá sempre o mesmo valor. São quadrados mágicos de 3x3.
Clique na imagem abaixo para jogar!
terça-feira, 1 de março de 2011
Multiplicação - Quando funciona e como utilizar
Por Roberto Perides Moisés e Luciano Castro Lima*
Ao lado da adição, da divisão e da subtração, a multiplicação é uma das quatro operações fundamentais da aritmética. Entenda como funcinoa essa operação. Imagine que numa adega estão armazenados vários tonéis de vinho. Cada parede da adega possui quatro prateleiras e em cada prateleira cabem seis tonéis. Dá muito trabalho contar todos os tonéis, um a um. Também é lento e dá trabalho somar - uma a uma - as parcelas iguais de tonéis distribuídos em cada prateleira.
A solução encontrada para esse tipo de problemas é o princípio multiplicativo: construir um retângulo imaginário composto de quatro prateleiras, cada uma delas abrigando seis tonéis.
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
Quando utilizar?
Veja um exemplo típico de situação em que a multiplicação é utilizada:
Cida tem no seu guarda roupa três saias para cada dia da semana.
Aplicando o retângulo do princípio multiplicativo, teremos uma figura cujo comprimento são os sete dias da semana e a largura são as três saias:
A partir daí, é possível deixar de lado as palavras usuais e ficar só com as "palavras matemáticas": Sete vezes três, ou 7 x 3.
O sinal que indica a multiplicação (X) não é a letra xis, mas sim dois riscos cruzados. Trata-se das duas diagonais do retângulo multiplicativo que se lêem como "vezes" ou "por": 7 x 3 (sete vezes três ou sete por três).
Por enquanto a sentença matemática está expressando apenas o movimento de ordenar as 3 saias para cada um dos 7 dias da semana. Os algarismos 3 e 7 constituem os fatores da multiplicação. Para indicar o que resulta desta operação numérica usamos o sinal = (lê-se igual).
Quando os matemáticos passaram a usar a letra x (xis) em seus cálculos, foi necessário substituir o x da multiplicação por um outro sinal para evitar confusão. E o sinal escolhido foi o ponto (.)
*Roberto P. Moisés é mestre em educação matemática (USP) e prof. do Col. Santa Cruz e das Universidades Sumaré e São Judas.Luciano Castro Lima é coordenador de matemática do Ceteac - Centro de estudos e trabalho em educação e cultura.
Copyright UOL. Todos os direitos reservados. É permitida a reprodução apenas em trabalhos escolares, sem fins comerciais e desde que com o devido crédito ao UOL e aos autores.
Assinar:
Comentários (Atom)











